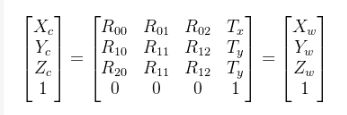以下的原理就是鱼眼坐标转世界坐标,世界坐标转鱼眼坐标的流程就是以下的反向推导。
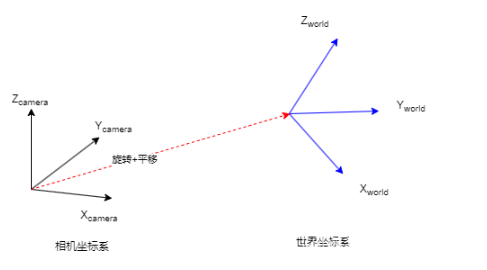
相机坐标系的定义:相机坐标系是以相机为基准建立的坐标系。它通常将相机的光学中心作为原点,相机的光轴为Z轴,X轴和Y轴与图像平面平行,与光轴垂直,形成一个右手坐标系。
世界坐标系的定义:世界坐标系通常是以某个固定的参考点、参考物体或参考方向为基准建立的。这个参考点可以是任何合适的选择,具体取决于应用的领域和需求。例如,在机器人学中,世界坐标系的原点可以选择为机器人基座的中心,或者是机器人末端执行器的中心。在地理信息系统中,世界坐标系的原点通常选择为地球的某个地理位置,例如经纬度为 (0, 0) 的点。
我理解的相机坐标系转换到世界坐标系的过程就是手眼标定过程,手指的是机械臂,眼指的是相机。



鱼眼坐标转世界坐标的主要原理就畸变矫正和坐标系的变换。
畸变矫正模型
1、平面相机的成像和坐标系如下所示
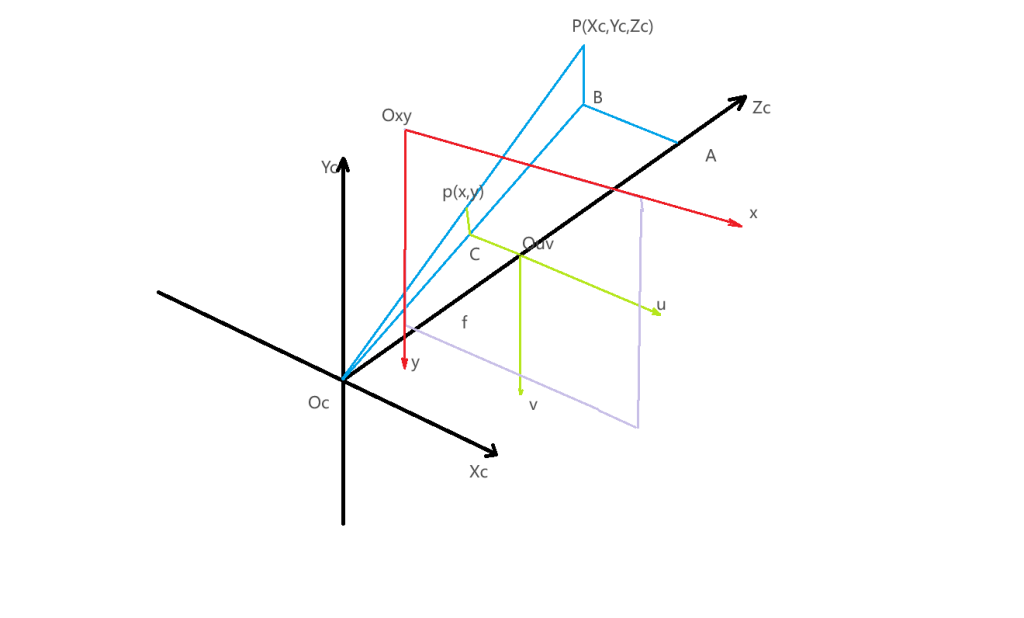
说明
1、f(ud,vd)就是以图像中心为原点坐标(和p(x,y)坐标相对,就是坐表原点不同)。
2、p(x,y)就是在图像坐标系下的坐标点,坐标点的为图像的左上角点,这个和世界图像的保存数据的坐标一直。
3、假设xy坐标系的原点是uv坐标系的中点,相对的偏移量为cx和cy,就可以得出ud=x+cx,vd=y+cy。
4、P(Xc,Yc,Zc)就是相机坐标系下的坐标。
根据相似的三角形可以得出
AB/COuv=AOc/OcOuv=PB/pC=Xc/ud=Zc/f=Yc/vd
得出
Xc/ud=Zc/fx
Yc/vd=Zc/fy
得出
ud=fx(Xc/Zc)
vd=fy(Yc/Zc)
得出
x=fx(Xc/Zc)-cx
y=fy(Yc/Zc)-cy
2、鱼眼相机的成像坐标变换
参考:https://ww2.mathworks.cn/help/vision/ug/fisheye-calibration-basics.html
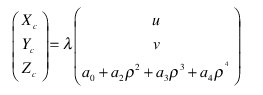

由上述的公式可以得出
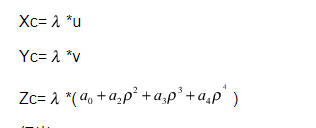
当
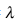
为1的时候得出相机的坐标是
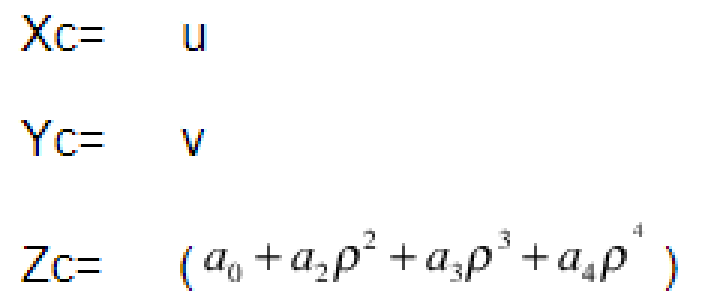
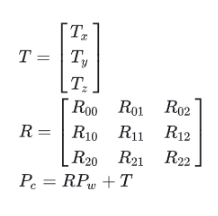
此时就可以计算出相机的坐标,在根据坐标系的变换就是坐标点的旋转和平移,此时定义的相机坐标系和世界坐标系是相同的原点,所以不存在平移矩阵就是旋转矩阵。一下的平移矩阵就都是0。