一、序言
在机器视觉中,涉及到三维定位的问题我们很大程度上会遇到从相机坐标系转换到机械臂坐标系,这篇文章讲述一下关于图像三维空间坐标系变换的相关知识。
二、相关知识点
1、位置的表示:
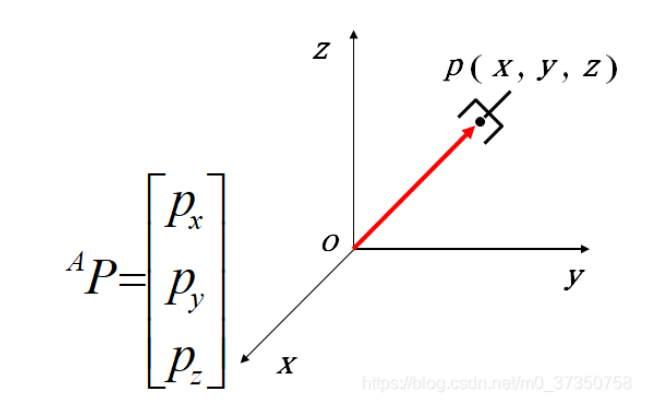
坐标系建立后,任意点p在空间的位置可以用一个3×1的位置矢量来描述;例如,点p在三维坐标系中表示为:
其中px,py,pz为P点的坐标分量(位置矢量不同于一般矢量,它的大小与坐标原点的选择有关)。
2、不同三维坐标系之间的转换关系
(1)平移
设坐标系{i}和坐标系{j}具有相同的姿态,但他俩的坐标原点不重合,若用3×1矩阵iPjorg表示坐标系{j}的原点相对坐标系{i}的位置,则同一点P在两个坐标系中的表示关系为:
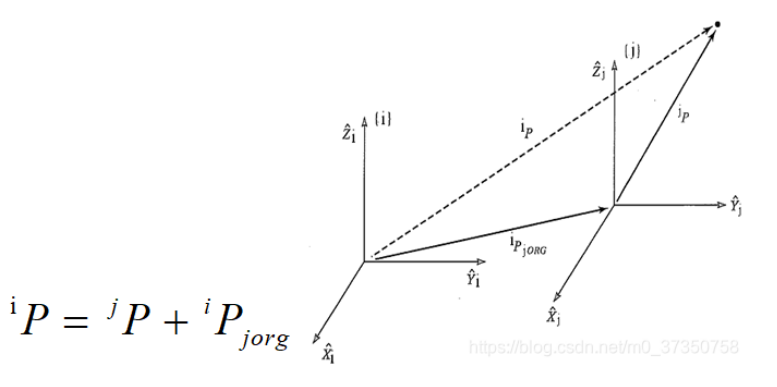
(2)绕z轴旋转角
坐标系{i}和坐标系{j}的原点重合,坐标系{j}的坐标轴方向相对于坐标系{i}绕z轴旋转一个角(
角的正负一般按右手法则确定,即由z轴的矢端来看,逆时钟为正)。
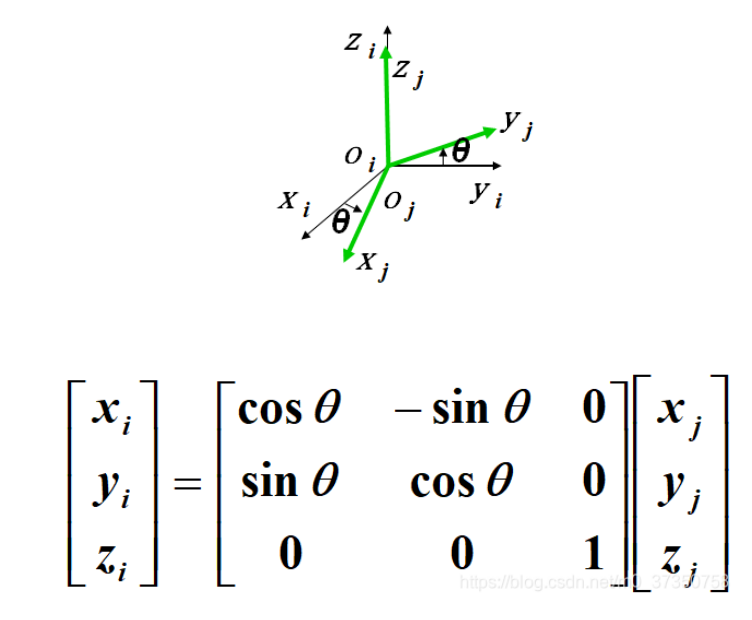
令:
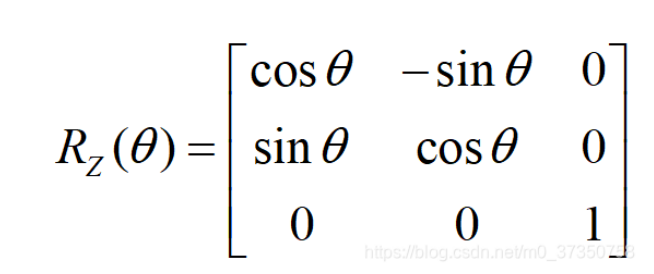
(3)绕x轴旋转α角的旋转变换矩阵为:
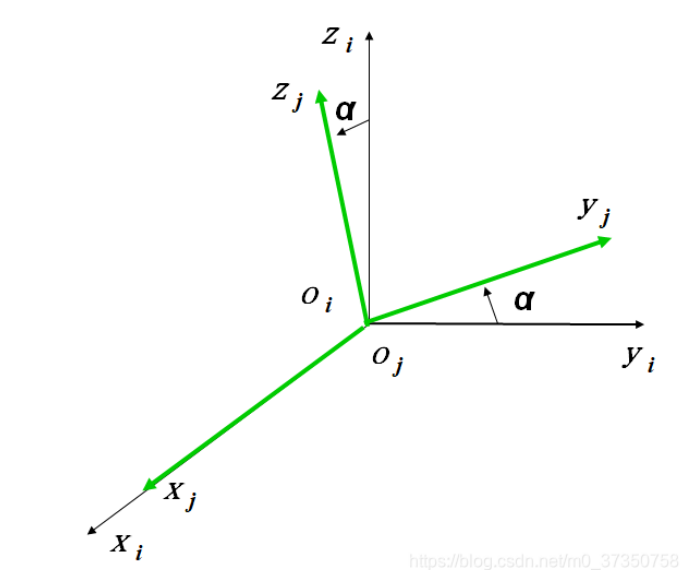
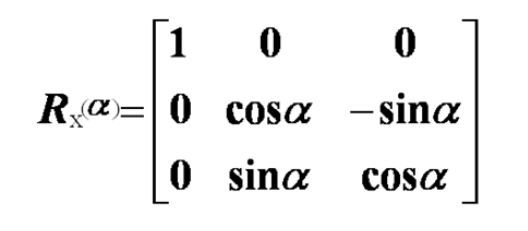
(4)绕y轴旋转β角的旋转变换矩阵为:
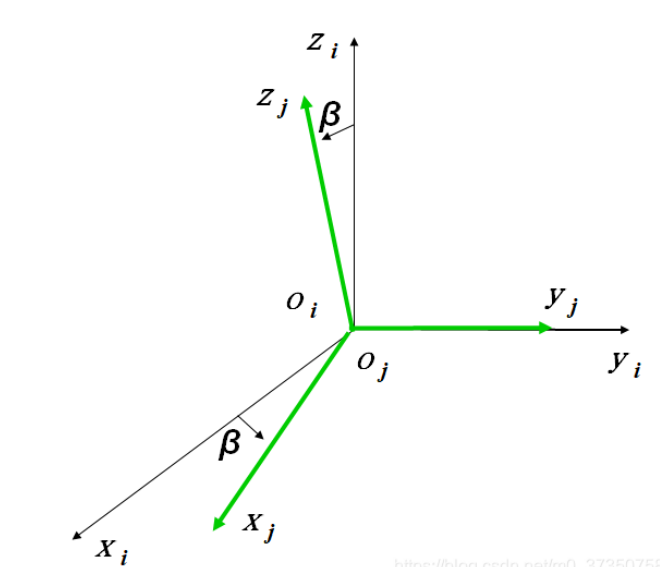
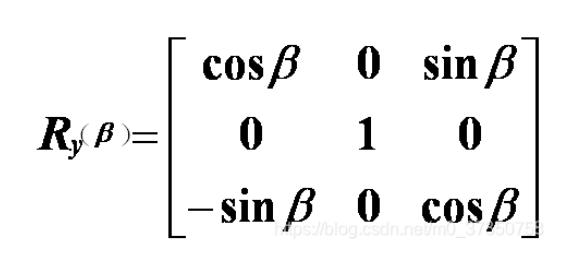
(5)复合转动
(本算法使用)
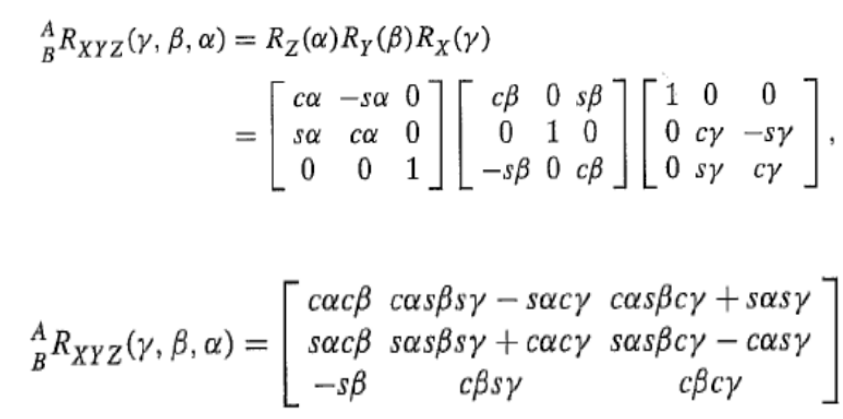
(6)绕任意轴转动
设绕k轴转动角,则旋转矩阵为:
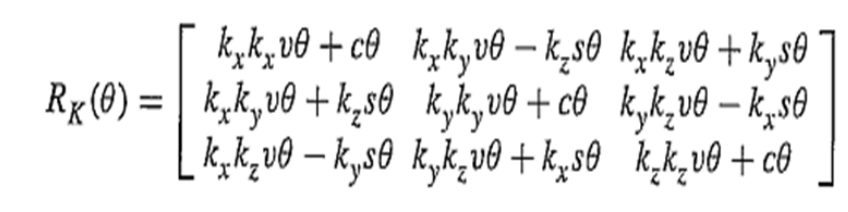
其中:
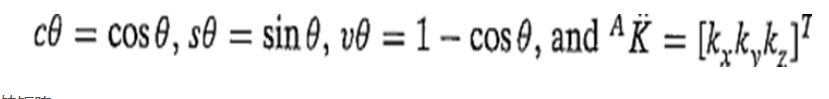
若给出一定旋转矩阵:
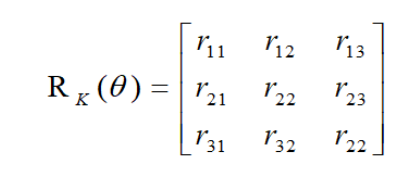
则可计算出:
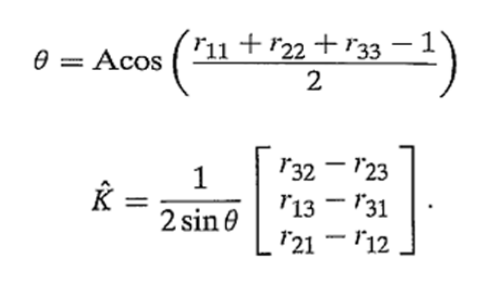
-=||=-赞 (5)